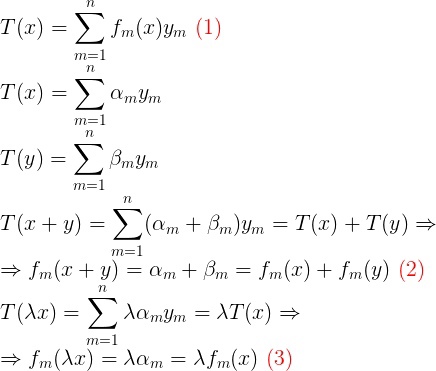Домашка по функану
Непрерывный оператор T из X в Y называется оператором конечного ранга, если T(X) конечномерно, где X, Y - банаховы пространства. Задача: Покажите, что любой оператор конечного ранга имеет вид (1), то есть, что для любого T существуют такие f_m и y_m. Решение: Возьмем в качестве y_m базис T(X), а в качестве f_m(x) - коэффициент \alpha_m при y_m в разложении T(x). Так как y_m базис, то разложение существует и единственное, так что функция определена всюду и корректно. Остается проверить, что f_m - действительно непрерывный линейный функционал. Линейность проверяется легко(2, 3), остается непрерывность. Тут у меня возникли проблемы, поэтому я неоч уверен в доказательстве. Заметим, что T(X) конечномерно, а значит изоморфно сопряженному пространству T(X)* с координатными функционалами, но действующими на T(X). Назовем функционал, соответствующий y_m как g_m. Отсюда f_m = g_m T, значит f_m - непрерывен, как композиция непрерывных функционалов. QED (непрерывность g_m я (не точно) проверил через изоморфизм T(X) и \mathbb{R}^n и эквивалентность по норме и тут хз)
PS: По условию y_m вектора из Y и f_m из X*