Основные понятия теории категорий

Как подготовка к другим статьям и как попытку понять теоркат я пишу это статью. Здесь будут базовые конструкции теории категорий. Также постараюсь в конце всяких определений приводить ссылку на ncatlab.org, своеобразная вики для теорката, чтобы можно было уточнить непонятные моменты и иметь ресурс авторитетнее автора. В конце будет определение функтора, так как это тоже главное понятие теорката, но, чтобы описать, как функтор обобщает все описанные в этой статье понятия, придется писать отдельную статью про пределы. Итак начнем.

Предел(здесь его не будет), копроизведение и неправильный pushout

Множество разделов математики работает с теми или иными обьектами и преобразованиями между ними. И множество вещей, связанных с ними так или иначе похожи. Теория категорий появилась, как способ обобщить все эти обьекты.

Определим категорию. Категория $\mathcal{C}$ это два множества: $\mathcal{Ob}(\mathcal{C})$ — множество обьектов категории, Hom(A, B) — множество стрелочек(морфизмов, функций), возможно пустое, между двумя обьектами A и B для всех пар обьектов и способ соединять стрелочки естественным способом, называемый композицией. Стрелки и морфизмы я, возможно, буду называть по разному, но это абсолютно одно и то же. Проще было бы назвать теорию категорий archery(стрельбой из лука), как писал один автор учебника по теоркату.

Категории, как и функторы, я буду обозначать жирным шрифтом, как вы уже могли заметить, Hom — это уже некий функтор. Обьекты будут обозначаться заглавными латинскими буквами, стрелки — строчными. Естественные преобразования греческими буквами, в общем все по дефолту.

Также есть аксиомы, которым должна подчиняться любая категория:

Существование композиции: для любых двух стрелок $f:A\to B$, $g:B\to C$ определена их композиция $g ∘ f:A\to C$, о котором можно думать, как о примененном сначала морфизма $f$, а затем $g$, хотя $f$, $g$, $g ∘ f$ это необязательно функции в привычном понимании. Также может вызвать вопрос о порядке стрелок в композиции, но он всегда был таким, стоит привыкнуть сразу.
Ассоциативность композиции: для любых трех стрелок $f:A\to B$, $g:B\to C$, $h:C\to D$ две композиции совпадают: $(h ∘ g) ∘ f = h ∘ (g ∘ f)$. Совпадают означает, что это суть есть одна и та же стрелка.
Существование единицы: для любого обьекта $A$ есть стрелка $1ᴬ$($A$ должна быть снизу, но тут проблемы с форматированием) такая, что для любой функции $f:A\to B$ выполняется $f ∘ 1ᴬ = 1ᴮ ∘ f = f$

Начала стрелок называются domain(домен) а конец codomain(наверное кодомен) и обозначаются так: для $f:A\to B$ имеем $dom(f) = A$ и $cod(f) = B$.

https://ncatlab.org/nlab/show/category

Далее композиция будет обозначаться без символа $∘$ по подобию произведения.

Примеры

Видно, что для определения категории достаточно определить множество обьектов, стрелок между ними и композицию. Как доказательство применимости теории категорий и для наглядности, приведем примеры некоторых категорий, не указывая, как строится композиция:

Категория 1: один обьект, одна его единичная стрелка.
Категория 2: два обьекта, одна стрелка между ними.
Категория 3: три обьекта, условно $A$, $B$, $C; две стрелки — $f:A\to B$, $g:B\to C$, $gf:A\to C$.
Категория множеств $\mathcal{Sets}$: обьекты — множества, стрелки — отображения.
Категория отношений $\mathcal{Rel}$: обьекты — множества, стрелки — отношения.
Категория графа: обьекты — вершины, стрелки — пути(не ребра).
Категория графов $\mathcal{Graph}$: обьекты — графы, стрелки — гомоморфизмы графов.
Категория топологических пространства Top(как уже заметно, категории называются по первым трем буквам, и топологии здесь повезло): обьекты — топологические пространства, стрелки — непрерывные отображения.
Категория частично упорядоченного множества(по другому poset), обозначения нет, так как категория строится на основе конкретного множества с частичным порядком: обьекты — элементы множества, стрелка между A, B — отношение неравенства A ≤ B.
Категория частично упорядоченных множеств $\mathcal{Pos}$: обьекты — частично упорядоченные множества, стрелки — монотонные отображения.
Категория категорий $\mathcal{Cat}$: Обьекты — локально малые категории, стрелки — функторы.
Категория банаховых пространств $\mathcal{Ban}$: обьекты — банаховы пространства, стрелки — непрерывные линейные операторы.
Категория гильбертовых пространств: обьекты — гильбертовы пространства, стрелки — непрерывные линейные операторы.
Категория группы, строится на основе конкретной группы: обьект — один единственный, стрелки — элементы группы.
Категория групп $\mathcal{Grp}$: обьекты — группы, стрелки — гомоморфизмы.
Категория абелевых групп $\mathcal{Ab}$: обьекты — абелевы группы, стрелки — гомоморфизмы.
Категория моноида, строится так же, как и категория группы.
Категория моноидов $\mathcal{Mon}$: обьекты — моноиды, стрелки — гомоморфизмы моноидов.
Категория лямбда выражений: обьекты — типы, стрелки — функции.

Можно добавить еще много-много примеров, включая производные категории и заинтересованному читателю(коих я не видел) предоставляется право доказать, что каждый пример удовлетворяет аксиомам категории. Приведенные примеры, во-первых, показывают насколько много охватывает понятие категории, и, во-вторых, позволяет читателю выбрать, о какой конкретно категории думать, когда он будет представлять какие-либо описанные далее понятия. Проще в качестве такой категории взять $Sets$ или категорию лямбда выражений, но также полезно думать о категории частично упорядоченного множества, так как конкретные примеры понятий там отличаются от тех же в $Sets$. В этом и есть одна из «сил» теории категорий — описывать разные понятия одинаковым образом.

Тизер

Все понятия будут описываться парами, так как одно понятие будет получаться из другого просто обращением стрелок, что дает нам такое понятие теорката, как дуальность. Причем первым понятием всегда будет в некотором смысле «предельным», а вторым — «копредельным».

Также почти все понятия будут описываться с использованием какого-то универсального свойства или по другому UMP(universal mapping property), что означает, что у нас в том или ином виде будет появляться существование и единственность какой-то стрелки. Все стрелки, удовлетворяющие тому же свойству, что и стрелка из UMP, совпадают с ней в силу единственности, что дает еще один способ уравнивать стрелки.

И, наконец, в теории категорий часто используются диаграммы, примеры которых можно увидеть в начале статьи. Они используются для формулировок, визуализации свойств и даже доказательств. Доказательство через диаграмму называется diagram chasing. Обьекты представляются в виде букв и стрелки в виде стрелок. Говорят что «диаграмма коммутирует» если любая композиция вдоль любого пути от одного обьекта до другого всегда будет одним и тем же.

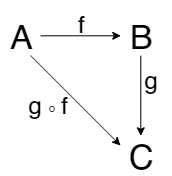
Например на этой диаграмме есть два пути из $A$ в $C$, а именно сначала через $f$, потом через $g$ или же сразу через их композицию $gf$. Понятно, что $gf$ это композиция $f$ и $g$, поэтому эта диаграмма комутирует. Пример посложнее:

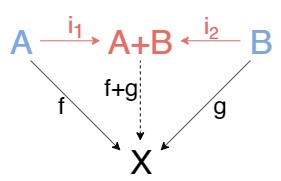
Если нам скажут, что эта диаграмма коммутирует(а она коммутирует), то мы из этого сможем понять, что $(f+g)i₁=f$ как два пути из $A$ в $X$ и $(f+g)i₂=g$ как два пути из $B$ в X. f+g это название стрелки, не пугайтесь, мы не умеем их складывать.

Также для облегчения восприятия определений я использую следующие обозначения в диаграммах: — обьекты и стрелки, на основе которых строится понятие, имеют синий цвет — определяемые обьекты и стрелки имеют красный цвет — произвольные обьекты и стрелки для UMP имеют черный цвет — и наконец стрелка из UMP свойства будет выделена пунктиром

Терминальный, инициальный обьекты

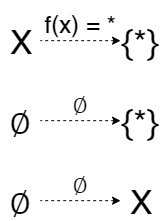
Терминальным обьектом называется обьект 1, для которого выполняется следующее UMP: для любого обьекта X существует единственная стрелка в 1, обозначаемая, как !ₓ:X\to 1. Другими словами, это обьект в который можно попасть из любого обьекта. Этот обьект вместе с инициальным обозначается не заглавной латинской буквой а единицей, но не следует его путать с единичными стрелками.

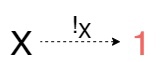Начнем с простого

Теперь инициальный обьект 0: им называется такой обьект, что для любого обьекта X есть стрелка ?ₓ:0\to X. Для этой стрелки я не нашел общепринятого обозначения поэтому обозначил ее как '?' в противоположность терминальному обьекту. По другому, это обьект из которого можно попасть в любой обьект.

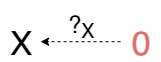Обратили все(одну) стрелки

В категории множеств 1 это множество с одним элементом, а 0 — пустое множество. Почему это так? Рассмотрим сначала любое одноэлементное множество 1. Для любого другого множества X мы сможем найти только одно отображение в 1, которое и дает этот единственный элемент. Единственная проблема возникает когда $X$ пусто. Но мы мало того, что утверждаем, что это отображение ∅\to 1 есть, но оно еще и есть для любого другого обьекта помимо 1. Это отображение это ничто иное, как пустое отображение! Если вспомнить формальное определение отображения из множества $A$ в $B$, что это множество пар элементов из $A$ и $B$, в котором для любого элемента $A$ существует единственная пара с его участием, тогда вполне можно утверждать, что пустое множество это отображение из пустого множества!

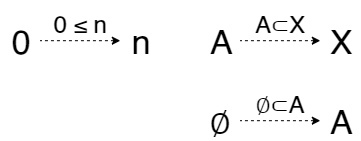
В категории любого poset-а 1 это, очевидно, максимальный обьект среди всех, в то время как 0 — минимальный среди всех, если они существуют. Это обьясняет их названия как 1 и 0, если считать, что у нас числа от 0 до 1. Пример poset-а в виде натуральных чисел. В категории этих чисел существует 0(терминальный обьект): это 0(число), если мы включаем его в натуральные числа, или 1(число), если не включаем. Максимального элемента в натуральных числах нет, если не включать бесконечность. Также можно рассматривать как poset множество подмножеств множества $X$ с отношением включения, тогда пустое множество снова будет 0, однако 1-ей будет все множество.

Внимательный читатель заметит, что одноэлементных множеств, минимальных и максимальных элементов может быть много, но, как несложно показать, они все изоморфны. Что это значит, далее.

https://ncatlab.org/nlab/show/terminal%20object https://ncatlab.org/nlab/show/initial%20object

Изоморфизм(дуален сам себе)

Стрелка $f:A\to B$ называется изоморфизмом, если существует(можно показать, что она сразу же и единственная) стрелка g:B\to A, такая что gf = 1ᴬ и fg = 1ᴮ. Два обьекта называются изоморфными, если между ними существует изоморфизм, и изоморфность(изоморфизм) есть отношение эквивалентности. Для изоморфных обьектов в таком случае пишут, что A≅B.

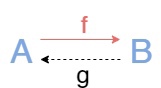Теперь стрелки две и если их обратить будет то же самое!

Эта диаграмма коммутирует, хотя казалось бы коммутировать тут нечему. На самом деле для удобства на диаграммах не показывают единичные стрелки, которые как раз и дадут равенства для изоморфизма написанные выше.

Изоморфизм это в каком-то смысле обратимое отображение, но сильнее. Суть в том, что имея в категории только обьекты и стрелки мы можем строить рассуждения используя только их. Но если мы что-то будем утверждать про какой-либо обьект, то мы сможем утверждать то же самое для любого изоморфного ему обьекта так как изоморфизм даст нам все что нужно для требуемых стрелок. Например, если мы скажем, что существует единственная стрелка с какими то свойствами из w:B\to X, и мы знаем, что A≅B, то и из A существует единственная стрелка с теми же свойствами. Строится она с помощью изоморфизма: wf:A\to X.

В случае множеств изоморфизм это биекция. Соответственно изоморфные множества это равномощные множества.

В случае poset-а — изоморфные обьекты это эквивалентные обьекты, то есть такие обьекты x, y, что одновременно x ≤ y и y ≤ x. В простейшем случае это равные обьекты, но в общем случае это может быть не так.

Например в теории принятия решений рассматривается задача нахождения оптимального результата. Приведу наитупейший пример. Вы хотите добавить сахар в чай, чтобы он был максимально вкусным. Понятно, что при увеличении сахара до некоторого момента чай будет вкуснее, но затем его будет слишком много. Мы можем утверждать, что 1000 грамм сахара ≤ 1 грамма сахара, в том смысле, что 1 грамм предпочтительнее 1000. Однако сложнее сравнить 4 и 5 грамм сахара, проще сказать, что нам безразличен выбор между ними, то есть 4 ≤ 5 и 5 ≤ 4. То есть выбор 4 и 5 грамм сахара эквивалентны, по другому 4≅5 или 4~5.

Если вы проходили алгебру или топологию, то можете попробовать вспомнить, что везде были понятия изоморфизма групп/векторных пространств/… или гомеоморфизм топологических пространств. Все это суть есть изоморфизмы в соответствующих категориях.

Как и сказано выше, терминальные и инициальные обьекты в категории $Sets$ и в категории любого poset-а изоморфны. Тривиально можно показать, что это так в произвольной категории, поэтому без разницы, какой именно обьект обозначать за 1 и 0, все свойства будут выполняться вне зависимости от выбора.

https://ncatlab.org/nlab/show/isomorphism

Мономорфизм, эпиморфизм

Стрелка $m:B\to C$ называется мономорфизмом, если для любого обьекта A и пары стрелок f,g:A\to B из равенства mf = mg следует f = g. Другими словами, если диаграмма коммутирует, то f=g. Еще: на него можно сокращать слева.

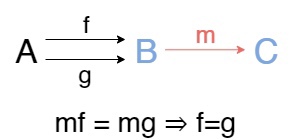Увеличиваем количество стрелок

Заметьте, что $f$ и $g$ в определении не фиксированы! UMP здесь нет, так как нет определяемого обьекта.

Дуально: $e:A\to B$ называется эпиморфизмом, если для любого обьекта C и любой пары стрелок f,g:B\to C из равенства fe = ge следует f = g. То есть, если диаграмма коммутирует, то f = g. Еще: на него можно сокращать справа.

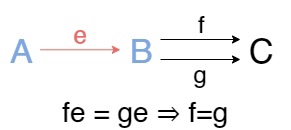Обращаем все стрелки

В категории множеств мономорфизм есть иньекция, эпиморфизм — сюрьекция.

Рассмотрим сначала мономорфизм. Чтобы понять, почему это иньекция, предположим, что это не так и возьмем в качестве A множество {x, y} из двух элементов множества B, для которых m(x) = m(y). Пусть f оставляет их на месте, т.е. f(x) = x, f(y) = y, а g меняет их местами, т.е. g(x) = y, g(y) = x. Так как $mf = m(x) = m(y) = mg$, то по определению мономорфизма имеем $f = g$, т.е. x и y обязаны быть одним и тем же элементом откуда получаем, что m — иньекция.

Теперь эпиморфизм. Возьмем в качестве C множество {0, 1} и в качестве f константу 1, а g определим так: g(y) = 1, если y принадлежит образу e, иначе g(y) = 0. Имеем fe = ge = 1. Значит f = g, и g переводит все элементы B в 1, то есть e — сюрьекция.

Мы знаем, что иньекция «вкладывает» одно множество в другое. Эту аналогию можно продолжить и ассоциировать мономорфизмы с «вложениями» их domain в codomain. Мономорфизмы в этом смысле характеризуют «подобьекты» других обьектов.

Хотя из иньективности и сюрьективности отображения следует биективность, в произвольной категории из того, что стрелка является и мономорфизмом, и эпиморфизмом, не следует, что она является изоморфизмом. Однако любой изоморфизм есть и мономорфизм, и эпиморфизм.

Также изоморфизмы, мономорфизмы и эпиморфизмы для краткости называются изо, моно и эпи соответственно.

https://ncatlab.org/nlab/show/monomorphism https://ncatlab.org/nlab/show/epimorphism

Product, coproduct(произведение, копроизведение/сумма)

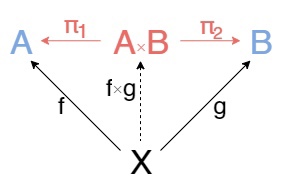
Для двух обьектов A и B их произведением называется обьект A×B вместе с парой стрелок-проекций: π₁:A×B\to A, π₂:A×B\to B. (само собой 1 и 2 в нижнем индексе). Причем такие(UMP), что для любого обьекта X с парой стрелок f:X\to A, g:X\to B существует единственная стрелка f×g:X\to A×B такая, что следующая диаграмма коммутирует.

+2

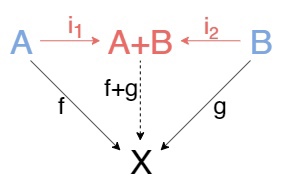
Суммой(аkа копроизведением) двух обьектов A и B называют обьект A+B с двумя стрелками-вложениями i₁:A\to A+B, i₂:B\to A+B, такими, что для любого обьекта X и пары стрелок f:X\to A, g:X\to B существует единственная стрелка f+g:X\to A+B такая, что диаграмма коммутирует.

Вращаю стрелки

В категории множеств произведение — декартово произведение. Проекции это проекции пар на первый и второй элемент соответственно: $π₁(a, b) = a, π₂(a, b) = b, f×g(x) = (f(x), g(x))$ Коммутативность:

\[ π₁(f×g)(x) = π₁(f×g(x)) = π₁(f(x), g(x)) = f(x) \\\ π₂(f×g)(x) = π₂(f×g(x)) = π₂(f(x), g(x)) = g(x) \]

Сумма же это непересекающееся обьединение, то есть обьединение множеств с добавлением метки из какого множества элемент пришел. Включения это добавления меток(обозначим метки, как :A и :B соответственно): $i₁(a) = a:A, i₂(b) = b:B, f+g(x:X) = X == A ? f(x) : g(x)$ f+g выбирает функцию на основе метки.

Даже для этой конструкции можно придумать много примеров, приведу еще один из программирования. Допустим у нас есть текстовые данные, содержащие разнотиповые данные, например числа, строки, массивы того или другого. Примером таких данных может быть формат JSON. Мы хотим распарсить JSON строку и что-то сделать, но мы не умеем работать с произвольным обьектом внутри JSON-а, но умеем работать с числами, строками и списками. И тут как раз поможет сумма этих функций, которая после разбора метки(который обычно делают через if-else проверку типов) применит нужную функцию!

В категории poset-а произведение — супремум двух элементов, а сумма — инфимум двух элементов. Напомню, что супремум это наименьший элемент, больший наших, и инфимум — наибольший элемент, меньший наших двух.

https://ncatlab.org/nlab/show/product https://ncatlab.org/nlab/show/coproduct

Equaliser, coequaliser(уравнитель, коуравнитель)

Здесь, хотя диаграммы и коммутируют, f не обязательно равно g.

Для двух обьектов A, B и двух стрелок f, g между ними эквалайзером называется обьект E и стрелка $e:E\to A$ такие, что $fe = ge$ и для любого обьекта X и стрелки m:X\to A, для которой выполняется равенство fm = gm, существует единственная стрелка u:X\to E такая, что следующая диаграмма коммутирует.

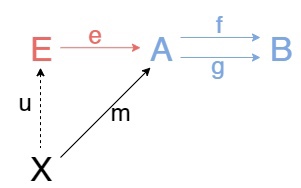-1 D; $m = eu$, то есть m раскладывается в композицию

Для двух обьектов A, B и двух стрелок f, g между ними коэквалайзером называется обьект Q и стрелка $q:B\to Q$ такие, что $qf=qg$ и для любого обьекта X и стрелки m:B\to X существует единственная стрелка u:Q\to X такая, что следующая диаграмма коммутирует.

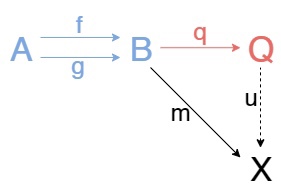Ну вы поняли, $m=uq$

Можно показать, что эквалайзер(которая стрелка) это всегда моно, а коэквалайзер всегда эпи.

Теперь обсуждение. Эти определения уже могут казаться сложными, хотя это опять таки обобщение уже известных понятий ядра и фактор-множества.

Рассмотрим категорию множеств. Эквалайзером в этом случае является множество $E = {x∈A | f(x) = g(x)}$, а e — вложение E в A, т.е. e(x) = x. Получается, что эквалайзер оправдывает свое название и просто заключает в себе все элементы, уравнивающие f и g. Если у вас вдруг найдется уравнение вида - $f(x) = g(x)$, можете просто взять соответствующий эквалайзер, который будет содержать все решения. Теперь про единственность и существование u. Если вдруг найдется какой-то обьект X с отображением m:X\to A как в определении, то мы имеем fm = gm. То есть для любого обьекта x из образа m имеем - $f(x) = g(x)$. Значит образ m есть подмножество нашего эквалайзера и мы можем вложить исходник этого образа(X) в эквалайзер с помощью отображения u. Теперь мы можем «описать» как действует m: сначала мы берем по элементу x множества X соответствующий элемент a = u(x) множества A, для которого - $f(a) = g(a)$, то есть «стандартизуем» x, а затем просто вкладываем его в A. Проще говоря, m = eu. Далее будет более конкретный пример с ядром.

Теперь коэквалайзер. Он, к сожалению, строится сложнее. Нам нужно взять минимальное отношение эквивалентности, в котором для любого x из A имеем f(x) ~ g(x). Тогда Q = B/~ фактор множество по этому отношению, а q — сопоставление классов т.е. q(y) = [y] класс y в фактор-множестве. Аналогично для любого X из определения оказывается, что X это что-то похожее, на фактор по отношению эквивалентности побольше, и потому содержит меньше классов. Мы можем вложить наши классы в «классы» из X отображением u. Тогда получим, что m сначала дает класс эквивалентности из коэквалайзера(отображением q), а затем по этому классу дает элемент X. По другому: m = uq.

«При чем же тут ядро?», спросит читатель. Все проще некуда. Возьмем категорию векторных пространств(или групп, или колец, или что вам больше нравится) и рассмотрим конструкцию эквалайзера еще раз. Если в качестве g взять константное отображение, дающее нулевой вектор, то эквалайзер это ничто иное, как ядро f!

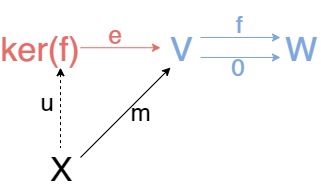
Понятно, что тогда если $fm = 0m = 0$(нулевой вектор), то $m$ всего-навсего выдает элементы ядра(эквалайзера) в зависимости от элемента X. Тогда мы можем это отображение перенести в само ядро, получая u. И получаем ядро f в чистом виде! Кстати необязательно ограничивать g, потому что можно получить эквалайзер как $ker(f - g)!$

Имея более конкретный пример эквалайзера, попробуем разобраться и с коэквалайзером. Снова возьмем в качестве g тождественный нулевой вектор. Каким бы ни был эквалайзер имеем qf = q0 = 0, так как q — линейное отображение и должно переводить нулевой вектор в нулевой вектор. Значит для любого y из образа $f (Im(f))$ имеем $f(y) = 0$ нулевой вектор в $Q$. Посмотрим, что у нас есть

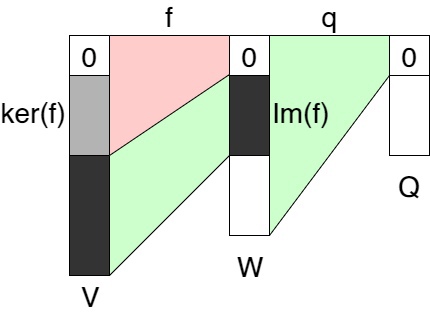Очень грубое изображение векторных пространств

Видим, что чем дальше, тем больше неизвестного: сначала элементы $W$, которые не получаются с помощью $f$, затем неизвестные классы в $Q$. Но не все так плохо! Мы знаем, что в фактор-пространстве W/Im(f) образ f как раз и является нулевым вектором. Так как нам нужно максимальное количество классов, то именно эта конструкция и даст нам коэквалайзер, который также называют коядром:

Такая же конструкция коядра строится в теории групп, колец и т.д. и изучается в алгебре.

В категории произвольного poset-а мы сможем построить не более одной стрелки между любыми двумя обьектами поэтому $f = g = A ≤ B$. После переобозначений получаем эквалайзер:

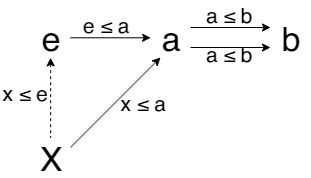
Видим, что обьект b никак не влияет на эквалайзер, и эквалайзер обьекта a это наибольший обьект, меньше или равный a, то есть сам обьект a. Коэквалайзер строится аналогично, ничего интересного.

https://ncatlab.org/nlab/show/equalizer https://ncatlab.org/nlab/show/coequalizer

Pullback, pushout(декартов квадрат и кодекартов квадрат)

Последний рывок.

Pullback для уголка из обьектов $A$,$B$,$C$ и стрелок $f:A\to C$, $g:B\to C$ это обьект $A×ᶜB$ с двумя стрелками $p:A×ᶜB\to A$, $q:A×ᶜB\to B$, такими, что $fp = gq$ и для любого обьекта претендента на трон pullback-a $Q$ с стрелками $m:Q\to A, n:Q\to B$, такими, что $fm = gn$, существует моно $u:Q\to A×ᶜB$, такой, что m = pu, n = qu. Т.е. следующая диаграмма коммутирует

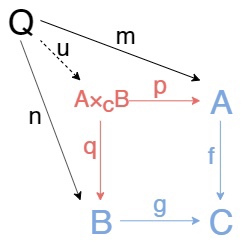
Другими словами, $m$ и $n$ раскладываются через $p$ и $q$ и один и тот же морфизм $u$ справа.

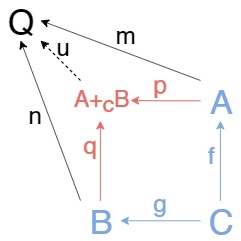
Pushout для уголка из обьектов $A$,$B$,$C$ и стрелок $f:C\to A$, $g:C\to B$ это обьект A+ᶜB с двумя стрелками p:A\to A+ᶜB, q:B\to A+ᶜB, такими, что pf = qg и для любого обьекта претендента на трон pushout-a Q с стрелками m:A\to Q, n:B\to Q, такими, что mf = ng, существует эпи u:A+ᶜB\to Q, такой, что m = up, n = uq. Т.е. следующая диаграмма коммутирует

Это база данных

Другими словами, $m$ и $n$ опять-таки раскладываются через $p$ и $q$ и один и тот же морфизм u, но теперь u слева.

Если вы ничего не поняли из определений, то могу предположить, что это уже не первый раз, так что приступим к разбору. Pullback можно на самом деле разложить в два уже известных обьекта: произведение с эквалайзером.

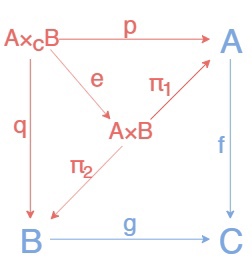
Для того, чтобы построить pullback на уголке мы можем сначала построить произведение $A×B$, а затем построить эквалайзер по обьектам A×B и C и двум стрелкам между ними $fπ₁, gπ₂:A×B\to C$. Этот эквалайзер вместе со стрелками $p = π₁e$ и $q = π₂e$ и даст нам в точности pullback.

Аналогично(дуально) можно построить pushout на уголке из суммы и коэквалайзера.

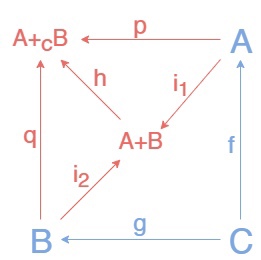
Сначала строим сумму A+B, затем коэквалайзер на стрелках $i₁f$, $i₂g:A+B\to C$. По аналогии получим pushout из стрелок $p = hi₁$, $q = hi₂$.

Отлично, теперь можно найти pullback-и и pushout-ы в разных категориях. Начнем с $Sets$. Произведение, как мы знаем, это просто множество пар элементов A и B. Соответствующие композиции для эквалайзера будут действовать так:

\[ fπ₁(a, b) = f(π₁(a, b)) = f(a) \\\ gπ₂(a, b) = g(π₂(a, b)) = g(b) \]

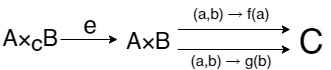
Далее, мы знаем, что эквалайзер это подмножество пар, на которых стрелки совпадают и вложение их в $A×B$. Соответственно $A×ᶜB = {(a, b)∈A×B | f(a) = g(b)}$. Осталось построить $p(a, b) = a$, $q(a, b) = b$ и мы получили pullback! Это всего лишь способ решать уравнения вида $f(x) = g(y)$ на функциях из разных множеств. Мы видели, что эквалайзер мог делать похожую вещь, но на функциях из одного и того же множества, а pullback может еще больше! Суммируя все полученное: pullback в категории $Sets$ для уголка $f:A\to C$, $g:B\to C$ это множество пар элементов из A и B, на которых f и g совпадают.

Очередь pushout-а. Сумма это непересекающееся обьединение с стрелками, добавляющими метки.

\[ i₁f(x) = i₁(f(x)) = f(x):A \\\ i₂g(x) = i₂(g(x)) = g(x):B \]

Напомню, что $:X$ это просто добавление метки и ничего более.

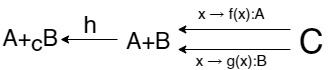
Далее вспоминаем, что коэквалайзер это фактор множество которое строится с грустью и болью, но все таки строится. Для взятия фактор множества мы должны взять минимальное отношение эквивалентности, в котором для любого x из C имеем f(x):A ~ g(x):B. То есть мы должны сопоставить любые два элемента, у которых совпадают прообразы, но так как отображения всего два, то в любом классе эквивалентности будет не более двух элементов. Все оказалось проще, чем мы думали! Приведу еще картинку по аналогии с коэквалайзером для векторных пространств, чтобы возможно стало понятнее, что к чему:

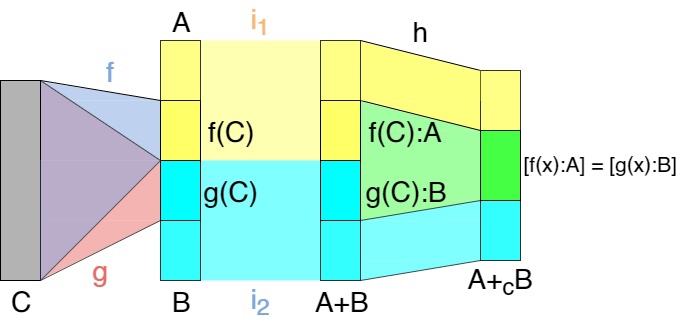Это почти полная диаграмма pushout-а лол

Видно, что образы f и g сопоставляются в силу эквивалентности, а остальные элементы A и B, которые не принадлежат образам f и g образуют свои классы. Получаем в итоге, что pushout в $Sets$ это способ «сопоставить» элементы в A и B с помощью отображений f и g. Время для тупого примера: пусть C — множество квадратов(фигур), A — множество прямоугольников, B — ромбов, f, g — вложения. Тогда pushout просто сопоставит квадраты среди прямоугольников с соответствующими квадратами среди ромбов.

Функтор

Теперь понятие, которое так или иначе проскальзывало раньше, а именно Hom и произведение на и сумма с фиксированным обьектом являются частными примерами функторов.

Функтором $F:A\to B$ между двумя категориями A и B называется отображение обьектов и стрелок A, такое, что все, что нужно, сохраняется. А именно стрелки вида $f:A\to B$ переводится в стрелку $F(f):F(A)\to F(B)$. Также сохраняются композиции и единичные стрелки.

Теперь если мы возьмем категорию всех категорий $\mathcal{Cat}$, то категории составят в ней обьекты, а функторы — стрелки. Однако, как предостерегает нас Кантор, не все так просто и не все категории могут быть обьектами в $\mathcal{Cat}$, а только локально малые, то есть те, в которых стрелки между любыми двумя обьектами составляют множество. В любом случае мы не будем углубляться в формализм так как все используемые категории(кроме может быть самого $\mathcal{Cat}$) локально малые и потому они есть в $\mathcal{Cat}$.

https://ncatlab.org/nlab/show/functor

Заключение

На этом пока что все. В качестве дз(хаха) можете подумать, про все приведенные понятия в разных категориях.

Что почитать

Невероятно, но до меня и так написано множество материалов по теоркату, так что не вижу смысла приводить их. Они легко гуглятся. Приведу некоторые ссылки, которые могут быть полезными: