Не просто корреляция

Корреляция в статистике это способ измерить, насколько связаны два фактора. Например корреляция Пирсона — это число от -1 до 1, которое означает тесную степень связости при приближении этого числа к -1 или 1, но слабую, если корреляция близка к 0. Знак этой корреляции говорит, связаны ли величины положительно или отрицательно, то есть при увеличении одного фактора будет другой фактор увеличиваться или же уменьшаться.
Однако проблема с корреляцией Пирсона в том, что она считается для двух количественных переменных, или как говорят дата саентисты(я) численных фич. Тем не менее, нам может быть интересно узнать, есть ли зависимость между фичами и целевой переменной если фича категориальная.
Еще раз про корреляцию
Посмотрим внимательнее на формулу корреляции Пирсона:
По сути это нормализация ковариации, в том смысле, что ковариация делится на произведение (корней из) ковариаций внутри переменных, откуда из неравенства Коши-Буняковского корреляция по модулю меньше единицы. Получается мы меряем (линейную) связь между переменными с помощью ковариации и затем нормализуем ее. А именно, если cov(X, Y) — большое число, то связь между переменными сильная, так как E(XY) за вычетом E(X)E(Y) все еще большое число и значит в произведении есть еще часть от произведения X и Y, которая остается в ковариации. Если же переменные почти независимы, то cov(X, Y) становится приблизительно равной E(X-EX)E(Y-EY)=(EX-EX)(EY-EY)=0, и коэффициент корреляции близок к 0.
Случай 1. Связь между категориальной и численной фичами
Тут имеет смысл попробовать также посмотреть величину отклонений(дисперсий) относительно среднего всей выборки и нормализовать, чтобы учесть величины дисперсий в каждом классе. Формально это можно записать так:
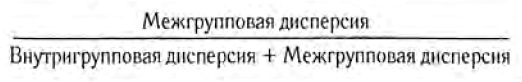
где числитель — это взвешенная дисперсия средних в каждом классе относительно среднего всей выборки, а знаменатель — сумма дисперсий по каждому классу плюс числитель. Веса это просто количество обьектов каждого класса.
Рассмотрим пример, есть оценки учеников по Анализу Данных по каждому полу(я хотел взять оценки по ЕГЭ, но этих данных не существует):
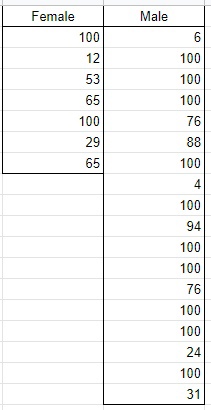
Всего в выборке 7 девушек и 18 мужчин. Посчитаем средние значения по каждому классу и для всей выборки:
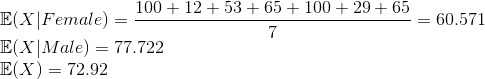
Почему я вспомнил про условное матожидание лол
Посчитаем дисперсии по каждому классу:
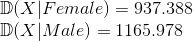
Омайгад, где поправка Бесселя, ты что крейзи?
Сумма дисперсий по каждому классу называется внутригрупповой дисперсией.
Найдем межгрупповую дисперсию:
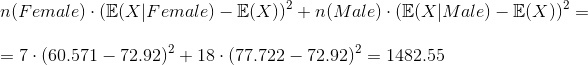
И наконец значение коэффициента корреляции, который, кстати, называется отношением корреляции:
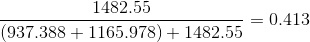
То есть связи слабая. Скорее всего у какого-то пола есть перекос в определенную сторону для оценки. Судя по приведенным выше данным(матожиданиям и дисперсиям) девушки склонны получать оценки меньше. Все еще можно проверить эту гипотезу на большей выборке, так как критерий p-значимости как считать я не знаю, как и не знаю достаточно ли приведенных данных. Плюс эти данные взяты из оценок по предмету в конце семестра, откуда и появилось много оценок 100, но возможно перекос в оценках также вызван этим.
Само по себе отношение корреляции всегда находится в пределах от 0 до 1, что очевидно из определения, и ее значения можно расценивать по следующей таблице:
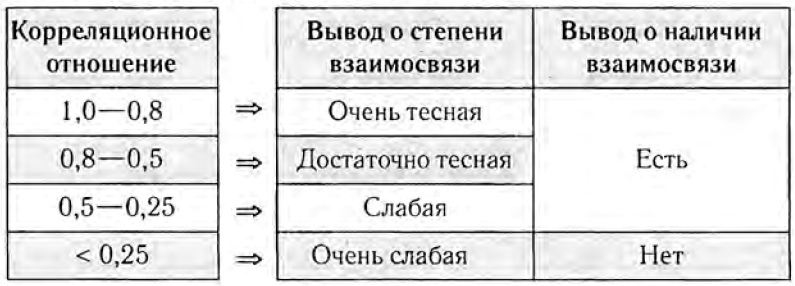
Случай 2. Связь между категориальной и категориальной фичами
Теперь у нас нет даже единственной численной фичи, а есть только категории. Но мы все еще хотим узнать насколько они связаны, то есть насколько принадлежность разным классам влияет на различие принадлежности к другим классам.
Сразу приведем формулу
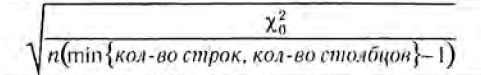
Этот коэффициент также находится в пределах от 0 до 1 и называется коэффициентом Крамера. Разберемся что здесь к чему:
n — количество всех обьектов в выборке
кол-во строк/столбцов — количество различных классов первой и второй фичи, из них берется минимум и вычитается 1
χ — критерий согласия хи-квадрат(также критерий согласия Пирсона). Кто не знает, хи-квадрат с k степенью свобод это распределение суммы квадратов k независимых нормально распределенных величин. Предполагая, что все величины в мире распределены нормально, мы можем захотеть изучить распределение их квадратов, например, чтобы не зависеть от их знака. Критерий хи-квадрат применяют, когда хотят проверить распределение случайно переменной относительно конечного числа промежутков.
Опишем, как посчитать этот критерий.
Для начала, количество обьектов каждой пары классов в нашей выборке, называется эмпирической частотой, потому что оно приближает реально распределение и получено с помощью эксперимента. Помимо этого, нам нужно найти количества обьектов каждой пары классов при условии независимости этих классов. Это количество называется теоретической частотой: какое в теории должно быть количество обьектов, чтобы связи не было.
Теоретическая частота для каждой пары классов считается как вероятность получить первым классом класс A, а вторым — класс X, если эти классы независимы(нулевая гипотеза H_0) умножить на количество всех обьектов. Для каждой пары классов A первой категориальной фичи и X второй категориальной фичи теоретическая частота считается по следующей формуле:
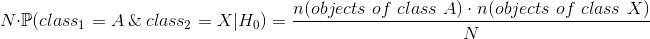
Где N — количество всех обьектов.
Затем для каждой пары классов считается число, которое затем в сумме по всем парам классов даст критерий хи-квадрат:
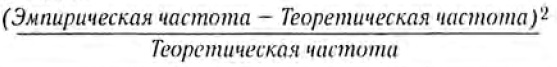
В итоге формула для критерия хи-квадрат следующая:

На всякий: n(…) это количество обьектов определенного класса(или классов) из нашей выборки, tf — теоретическая частота
Затем это значение подставляется в исходную формулу, где остальные переменные известны.
Приведем пример(из манги да): провели опрос среди читателей журнала с просьбой указать желаемый вид признания в любви из трех и свой пол. Получили следующие данные:
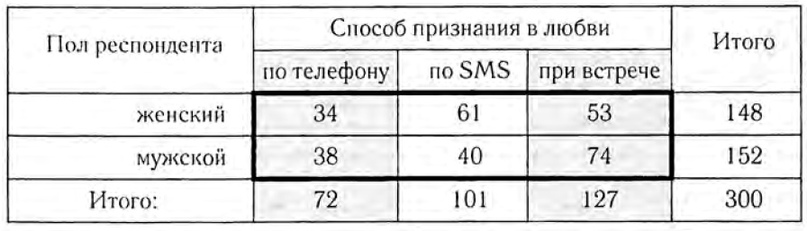
Выражения для теоретических частот для каждой пары классов. В каждом столбце внизу написано количество обьектов по способу признания, а справа для каждой строки количество обьектов для каждого пола. Формула для теоретической частоты в нашем случае: n(способ) * n(пол) / N, для каждой пары (способ, пол):
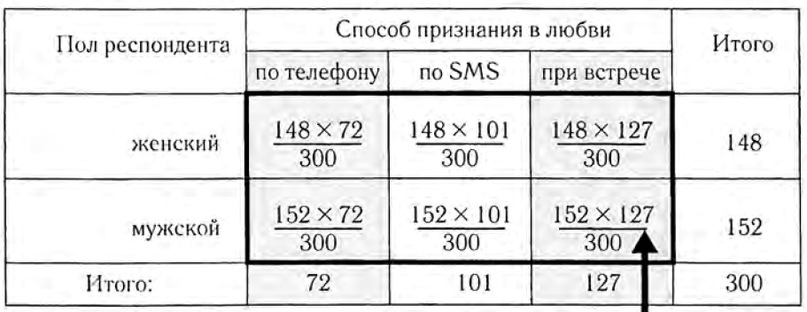
Находим коэффициент хи-квадрат:
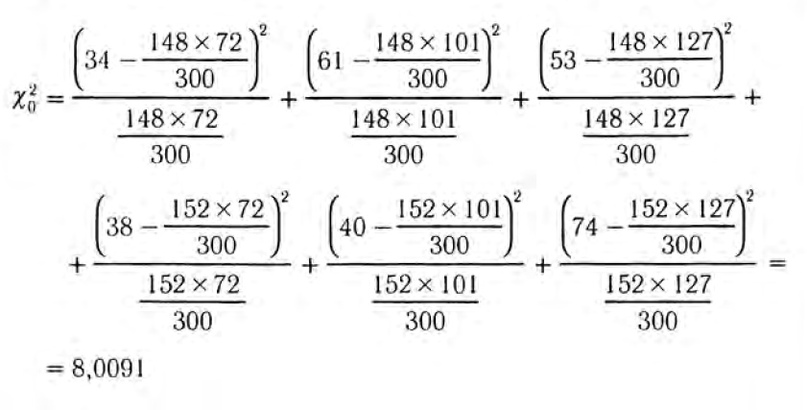
Подставим это значение в формулу для коэффициента Крамера:
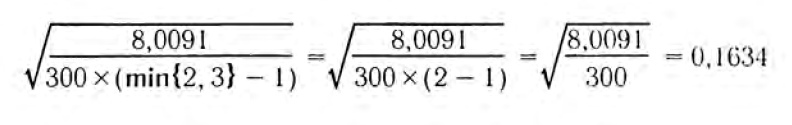
Получили значение, которое говорит об отстутствии связи. Другими словами не получится хорошо предсказывать желаемый способ признания для человека, зная только его пол. И наоборот, зная, какой способ признания нравится человеку(с которым вы например переписываетесь в интернете) определить его пол.
Таблица, для интерпретации тесноты связи та же, что и для отношения корреляции. Здесь коэффициент меньше 0,25 так что связь слабая. Вывод
Таким образом, если у вас есть категориальные значения, и вы хотите посчитать их связь с целевой переменной или классом, то не все так плохо! Соответствующие коэффициенты считаются за линейное время и позволяют также, как и корреляция Пирсона, говорить о связи переменных.
Мне же теперь придется использовать эти коэффициенты для оценок полезности в соревновании про дома и, возможно, других исследованиях.